2 جائزة ابل لرياضيات 2012 .... و الشيخ الهنغاري

لنفترض اني اعطيتك عزيزي القارئ مجموعة من اﻷوراق تحمل اعداد مرتبة من 1 الي n حيث عدد كبير بما فيه الكفاية ، وطلبت منك ان تنزع بعض من هذه اﻷوراق بصفة عشوائية . فهل تظن انك افسدت النظام السابق علي الترتيب ؟ ام انه ما زال هناك نظام  بحيث يستطيع ان نجد نظاما ما في داخل ذلك النظام المشوه بسحب اراقام اختيرت عشوائيا ؟
هل تسمح اﻷعداد التي كان يسودها النظام ان تفسدها اﻷيادي بسحب بعض من اعضائها ، ام ان رياضيات هي التي صنعت النظام وهي التي تحكمه ؟ في البداية اذا كانت اﻷعداد منتهية فانها لن يوجد نظام بداخلها او سيتوقف ولكن ماذا اذا كانت غير منتهية ؟  


 الجواب هو نعم يوجد دائما هناك نظام حتي لو كنا سنجده عند اعتبار اعداد كبيرة لغاية لكنه يوجد، والعهدة علي العالم الرياضيات الهنغاري اندر سزمريدي  Endre Szemerédi ، والثمن احدي اكثر الجوائز الرياضيات شهرة و مرموقية جائزة ابل (Abel Prize ) لرياضيات لعام 2012 .


ففي يوم 21 من الشهر الجاري قام ملك النرويج بتوشيح عالم الرياضيات الهنغاري Endre Szemerédi بجائزة ابل للرياضيات للعام 2012 وذلك حسب المجمع العلمي النرويجي"اعترافا بمجهوداتها في مجالات الرياضيات الغير متصلة و علم الحاسوب النظري و النظرية اﻷرجوية و نظرية اﻷعداد" الجائزة تصل قيمتها الي حوالي مليون دولار نقدا .
اندريه البالغ من العمر 71 عاما ، والذي نشر عبر مسيرته العلمية ازيد من 200 بحث علمي  والحاصل علي عدة جوائز سابقة ، يعتبر اهم اعماله العلمية تلك المتعلقة بنظربة الشهيرة Szemerédi's theorem  والتي تثبت انه يوجد في اي سلسلة اعداد متتالية عددية منتظمة ، 
و التي برهنها عام 1975 في عمل يزيد عن 200 صفحة و دخلت النظرية بقوة في اعمق اﻷفكار الرياضية و الفيزيائية علي حد سواء هذا باﻷضافة الي عدة اعمال معتبرة في مجال علم الحوسبة و نظرية الكمومية .


في الحقيقة ان نظرية سزمريدي اعمق بكثير و اكبر ومثال اﻷعداد الذي اعطيته مجرد محاولة لتقريبها او مثال لتطبيقاتها
 رغم ذلك لا يوجد لها تطبيق علي ارض الواقع لكنها اﻷسس التي اعتمدت عليها عدة تطبيقات تجعل  حياتنا اليومية اكثر راحة خاصة تطبيقاتها في مجال الحواسيب و الذكاء اﻷصطناعي بل وسمحت ﻷول مرة وباﻷعتماد علي بعض نتائجها ببناء روبوت قادر علي التعليم الذاتي....
كما انه برهانها لم يكن يوما سهلا فقط تطلب اكثر من 200  صفحة وعدد كبير من المبرهنات و اﻷستنتاجات و اﻷفتراضات
 الصورة التالية توضح بعض من ذلك حيث يرمز حرف T=نظرية L=نظرية تمهيدية  C=نتيجة مباشرة لنظرية D=تعريف 

كيف برهن سزمريدي علي نظريته

هذا باﻷضافة الي انه ثالث ثلاتة اخرجوا لعالم خوارزمية AKS التي تشير الي اﻷحرف اﻷولي من اسماء مكتشفيها التي تتيح معرفة ما اذا كان العدد اولي اما لا و تجد تطبيقات واسعة في تشفير المعلومات الذي يستخدم في كل اتصالاتنا.....  

الفتي الذي بدأ بدراسة الطب ثم قطع دراسته  وتحول الي العمل في مصنع قرر يوما ما ان يحصل علي شهادة دكتواره في الرياضيات فكان له ما اراد بل واكثر بعد ان اصبح من اعظم من مروا يوما ما بالرياضيات و الفيزياء و ربما العلوم اجمع.

تابع القراءة

0 الرياضيات و الجمال.... مثلثات سيربينسكي

حين يقوم عالم رياضيات او عالم فيزياء باعداد نموذج رياضي  لظاهرة فيزيائية ما فمن من غير المفاجئ ان تعبر عن تلك 
الظاهرة و ان تتطابق الي اقصي حد مع تلك الظاهرة ....
لكن المدهش حقا حين تتطابق فكرة مجردة مع واقع مشاهد لمجرد ان تلك الفكرة جميلة .....  
فاهلا بك في تدوينة خفيفة عن الرياضيات و الجمال
 تقول النظرية ان كل نظرية جميلة تتطابق و شيئا ما في عالمنا اليوم....
او بعبارة اخري ان كل ما هو جميل يوجد في عالمنا وبالتالي ما عليك الا ان تكتشف نظرية جميلة
 و سنتطبق علي شيئا ما من عالمنا  الجميل ، و اليك مثال.....
في عام 1915 قدم عالم رياضيات البولوندي Wacław Sierpiński ما عرف لاحقا بمثلثات سيربينسكي وهي تعتمد علي فكرة في غاية
البساطة لكنها تخرج شكلا في غاية الجمال ...

في  البداية نرسم مثلثا متساوي اﻷضلاع و بعد ذلك نرسم مثلثا وسطه عن طريق ربط منتصفات اضلاعه و نكرر نفس الشئ  حتي نصل الي النتيجة التي نرغب بها و الحد هنا هو دقة الشاشة التي ستعرضه....

مبدأ رسم مثلثات سيربينسكي -المصدر:ويكيبديا

المدهش في اﻷمر ان نفس اﻷشكال توجد و تحديدا عند اﻷسماك من نوع  حلزون البحر، انظر الشكل التالي...

تري هل فكر  سيربينسكي عندما اقترح مثلثاته انها توجد فعلا........

فسبحان من خلقها وصورها و جعلها عبرة لكل معتبر...

تابع القراءة

0 [خبر علي السريع] فريق تجربة ICARUS ....و الخبر اليقين

 في خبر متوقع نفي فريق تجربة ICARUS في الدراسة التي قام بها في مركز اﻷبحاث النووية باطاليا ان تكون النيترونات تجاوزت سرعة الضوء و هو الشئ الذي كانت مجموعة تجربة OPERA ادعته قي وقت سابق....

النص التالي هو اقتباس من ورقة بحثية قدمتها المجموعة :

والنتيجة التي توصلنا اليها متوافقة مع وصول المتزامن لجميع النترونات بنفس القدر من السرعة، اي سرعة الضوء. .
و لهذا فانه يوجد فرق صارخ مع النتيجة التي ذكرت OPERA ; التي ادعت أن النيوترونات ذات الطاقة العالية تصل CERN حوالي 60 نانوثانية قبل الموعد المتوقع من وصول الضوء.....

تابع القراءة

0 جميل جدا مثل π

في قطرات الندي و بين حركات الجفون في اﻷمواج وفي التذبذبات علي سطح الماء ، في الجينوم البشري و في اعماق الكون....
هناك عدد يفهمه كل ذلك الجمال و يترجم لنا كل تلك العجائب
 لكننا لا نستطيع فهم اغوار غموضه
 ولا فك جميع اﻷلغاز التي تحيط به انه  π .....
هذه  تدوينة عن النسبة التابتة  π وعلاقتها بالجمال وبالعلوم وبالرياضيات
  سنتحدث فيها باذن الله عن  π  ماهيته ، تاريخه ، جماله 








π  بالتعريف هو حاصل قسمة محيط الدائرة علي  قطرها و هو ثابت رياضي يرمز له برمز بـ π ﻷنه هو الحرف اﻷول من الكلمة 
اليونانية περίμετρος والتي تعني محيط شكل هندسي ما،
وقد عرف منذ ما يزيد علي 4000  عام عند البابليون و المصريون القدامي وفي بلاد الصين والهند و لكن  اول دراسة علمية جادة له كانت من طرف العالم اليوناني ارخميدس حوالي 200 عام قبل الميلاد  في كتابه "On the Measurement of the Circle" اول من اعطي تقريبه الي رقمين ما بعد الفاصلة  و  ذلك بوضع  متعدد اﻷضلاع  في دائرة و من ثم حساب محيط متعدد اﻷضلاع وتقريب محيط الدائرة له انظر الشكل 1

تقريب π  بحساب محيط متعدد اﻷضلاعالمصدر:ويكيبديا 

لم يكن ارخميدس في ذلك الوقت  يرمز له ب π بل كان يدعوه فقط بـ "محيط الدائرة الي قطرها " و يستمر الوضع  حتي القرن السابع عشر 
حين وضعت  علاقة لتقريب π من طرف العالم اﻷلماني Ludolphian ومن ثم يسمي π بــ ثابت Ludolphian و نجح بتقريبه الي 35 رقم
 ما بعد الفاصلة  ، اما اول من استخدم الرمز π فهو عالم الرياضيات والفيلسوف البريطاني  William Jones في العام 1706 في كتابه “A New Introduction to the Mathematics.”
  قبل ان يقرأ Leonhard Euler  الكتاب عام 1737 ويستمر في استخدام الرمز ليصبح اليوم الرمز المعتمد لتمثيل النسبة الثابتة 




π هو عدد غيرنسبي مما يعني انه لا يمكن كتابته علي شكل كسر مقامه وبسطه اعداد طبيعية و لكن يمكن فقط تقريبه باستخدام الكتابة
 العشرية له هذه الكتابة تثير للحد اﻷن عجائب هذا العدد ولا يعرف الرياضيون مما يوجد فيها لكنهم يتنافسون للمواصلة استكشافها اخر 
رقم  حطم في هذا المجال كان من طرف المبرمج الفرنسي   Fabrice Bellard  باكثر من 2700 بليون رقم ما بعد الفاصلة (1)
كما لا يمكن انشائه هندسيا ( مثل جذر 2 مثلا ) باستخدام خط مستقيم فهو  transcendenal شئ غامض تماما
 كما يقول الفيلسوف اليهودي موسى بن ميمون 

ينبغي ان نعرف ان نسبة محيط الدائرة الي قطرها ليس معروفا ولا يمكن حسابه بدقة ابدا وهذا ليس لقصور معرفتنا له أو اهمالنا

 لشئ  يتعلق بدراسته ، ولكن ﻷنه مجهول من طبيعته و اكتشاف لا يدرك ابدا

احيانا تجري المسابقات الرياضية في حفظ ارقام العدد وهذه اﻷرقام اﻷولي منه :

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091

من عجائب كتابته ان العدد المميز 0123456789 ظهر 6 مرات في الـ 50 بليون رقم اﻷولي من الكتابة العشرية للعدد π
بنما ظهر العدد 0987654321  خمس مرات في كتابته.....  


π يوجد في كل العلوم تقريبا و في كل القوانين اﻷساسية التي تحكم الكون من قانون التجاذب العام الي قانون اﻷرتياب هايزنبرغ الذي يحدد

مقدار اﻷرتياب عند حساب موقع جزيئ ما الي الثابث الكسمولوجي مرور باشهر ثوابت التي تحكم الكون....

  π واضح في كل شئ من حولنا من قرص القمر المدور الي شكل الشمس في رابعة النهار يختفي هنا  هناك من تقابل DNA الجينوم البشري

الي موجات الصوتية التي تدغدغ آذاننا كل حين و تلك  الكهرومغناطيسية التي تأمن اتصالاتنا في صمت ....

π يختزل الرياضيات بجمالها اللامحدود بغموضها و بطلاسمها التي لا تقبل الحل ولكنها تقبل التطبيق فقط...

ملاحظة : كتبت هذه التدوينة بمناسبة اليوم العالمي لتخليد π

 راجع هذه التدوينة   لمعرفة المزيد 

مراجع هذه التدوينة :

___________________________________________________________________________

Richard Preston , "THE MOUNTAINS OF PI" , The New Yorker  , 1929

As Easy As π", Joel Chan, University of Toronto , 2000"

"Jonathan M. Borwein, "The Life of Pi: From Archimedes to Eniac and Beyond

  Mathematics in Culture, 2007

 

  

تابع القراءة

0 غدا اليوم العالمي لنسبة الثابتة π

يصادف غدا 14 من مارس العيد العالمي المخلد للنسبة الثابتة المعروفة بـ  π 
وهي تظاهرة عالمية تشارك فيها عدة جامعات و مؤسسات تعليمية لتذكير بالنسبة الثابتة و اهميتها في العلوم وباﻷخص في علم الرياضيات...
اليوم العالمي لـ  π لمن لا يعرفه هو يوم اطلق عام 1988 من طرف الفيزيائي Larry Shaw من متحف سان فراسيسكو للعلوم في الولايات المتحدة اﻷمريكية ويستهدف تخليد النسبة الثابتة او  π....

اما  π فهو الحرف اﻷول من الكلمة اليونانية περίμετρος والتي تعني محيط دائرة في اللغة اليونانية و تم ورمز له  بـ π  من طرف William Jonest  في القرن الثامن عشر و اصبح الرمز شائعا بعد استخدام Euler له في عدة بحوث له ....
و اما تعريفه فهو  حاصل قسمة محيط الدائرة علي قطرها و قد عرف منذ ما يزيد علي 4000 عام عند الشعوب البابلية و الذين قربوه الي 3 اما اليوم فنعرف اكثرمن 3 ترليون رقم ما بعد الفاصلة للكتابة العشرية للعدد  π ....

ويتم تخليد اليوم العالمي للنسبة ثابتة يوم 3.14 ﻷنها اﻷرقام اﻷولي من العدد المقرب له ومن اهم اﻷنشطة المخلدة له المسابقة التي ترعاها ووردبريس  

و تضم مجموعة من اﻷلغاز و تمارين الرياضية الجميلةويمكنكم المشاركة فيها علي الرابط  

http://www.pidaychallenge.com/

كما سنكون غدا ان شاء الله في المناسبة لنكتب تدوينة عن اسرار النسبة الثابتة و علاقتها بالعلوم و الهندسة ..
عيدا سعيدا وكل عام و   π  اجمل .....

تابع القراءة

0 هل أقصر الطرق خط مستقيم ؟.... دراسة جديدة من MIT

احيانا يكون الطريق اﻷقصر بين نقطتين ليس الخط المستقيم الذي يربط بينهما كما هو الحال بالنسبة للغواصات اﻷلية التي تعمل في المحيطات خاصة اذا ما اخذنا في اﻷعتبار تاثير  التيارات المائية التي تتعرض لها الغواصة علي المسافة التي تقطعها وعلي كمية الطاقة التي تستهلكها لقطع هذه المسافة....
ففي دراسة حديثة لمجموعة من الباحثين من معهد MIT للهندسة تم اقتراح  طريقة جديدة تمكن من التنبأ باقصر الطرق و أكثرها حفاظا علي الطاقة  اذا ما تنقلت الغواصة من نقطة أ الي نقطة ب  وذلك باخذ تاثير التيارات المائية علي الغواصة اﻷلية و مقاومتها لها  بعين اﻷعتبار .....
المشكلة يمكن تلخيصها في ايجاد احسن الطرق لتنتقل الغواصة من النقطة أ الي ب باعتبارسرعتها الحدية وبافتراض سرعة تيار مائي ثابتة و هي مشكلة رياضية يتطلب حلها  خورازميات رياضية معقدة و برجمة غير خطية .....

وقد طبق الباحثون الطريقة الجديدة للحصول علي الطرق  اﻷقصر في حالة مجموعة  تتكون من 9  الغوصات و التي يظهر الشكل التالي مساراتها التسع و اقل شئ يقال عنها انها بدون شك غير مستقيمة ...

يذكر ان البحث سيتم عرضه في اجتماع IEEE المخصص لربوتات نهاية شهر مايو المقبل....
الفيديو التالي الذي نشره معهد MIT يسل الضوء علي بعض من جوانب البحث و النتائج المترتبة عليه....

تابع القراءة

0 مندليف و ميلاد الجدول الدوري

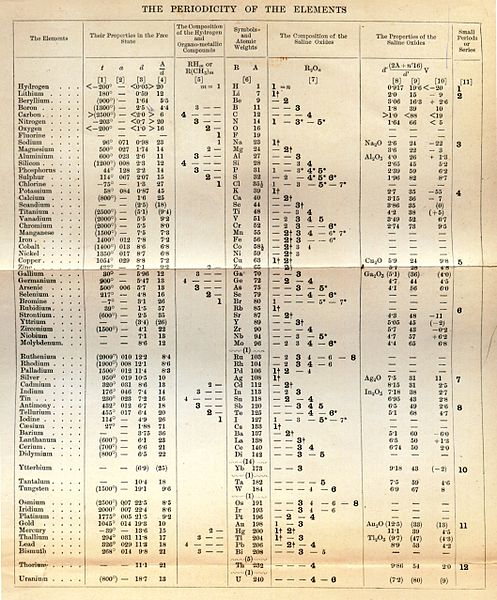
في مثل هذا اليوم من عام 1869 قدم عالم الكيميائي الروسي الصربي المولد ديمتري مندليف ورقة بحثه الشهيرة    أعتماد خواص العناصر على الكتلة الذرية  أمام المجمع الكيميائي الروسي ليخطو بذلك اﻷنسان خطوة جبارة في فهم الكون المحيط به و التحكم وفيه والتدبر في عجائب قدرة الخالق عز وجل...
  و قد تم نشر جدول مندليف في جريدة روسية غير معروفة، ولكن تم إعادة نشره في المجلة الألمانية Zeitschrift für Chemie في عام 1869 .وذلك قبل شهور قليلة من نشر الأبحاث المستقلة لكيميائي الألماني ليوس لوثر ماير والذي قام بنشر جدول معدل مشابه لجدول مندليف عام 1864. وقد توقع مندليف اكتشاف أخرى وأشار إليها وأشار إلى كتلها الذرية، كما ترك أماكن فارغة للعناصر التي كان يتوقع انها ستكتشف. لم يحتوى جدول مندليف الغازات النبيلة نظرا لأنها لم تكن قد اكتشفت بعد.


الجدول الدوري الذي نعيد نشره في نسخته اﻷصلية  :

 و نعقب عليه بقول مندليف :

لا يوجد قانون في الطبيعة يمكن تعميمه علي كل شئ ...... علاوة على ذلك،و فان اكتشاف قوانين الطبيعة  لا يحدث عندما نفكر لأول المرة من أنها تأخذ شكل من الأشكال، أو حتى عندما نعترف به، ولكن فقط عندما يتم تأكيد ذلك من خلال نتائج التجربة. يجب على رجل العلم  النظر في هذه النتائج و اعتبارها  الدليل الوحيد على صحة تخميناته وآرائه[2].

___________________________________________________________
[1]wikipedia
2]. J. Kendall, Young Chemists and Great Discoveries, Appleton-Century, New York, 1939, pp. 186-201.

تابع القراءة

0 مع HILBERT و مبادئ الهندسة الخمس

الرياضيات أم العلوم و أصلها وعالم الرياضيات الحقيقي هو من يعرف كيف يستخرج النتائج من المبادئ  و لكل فرع من الرياضيات مبادئ قليلة وبسيطة تسمي البديهات او المسلمات و هي نظريات استنتجناها من  تحليل منطقي  لعالمنا الملموس .
في هذه التدوينة سنتعرف علي المبادئ الخمسة او المسلمات التي بنيت علي اساسها الهندسة ، لذلك سنقوم في البداية بتعريف بسيط للهندسة و ثم سرد اقسامها و من ثم سنعرض مبادئها الخمسة التي تقوم عليها حسب رأي DAVID HILBERT احد اعظم علماء الرياضيات في القرن العشرين...
الهندسة الرياضية (Geometry) أحد فروع الرياضيات التي تتعامل مع العلاقات 
المكانية (الحيزية)، وما يمكن تشكيله من ارتباط نقاط الفراغ لتعطي ما يدعى بالأشكال 
الهندسية. في البداية كان الرياضيات فرعان فقط : دراسة الأعداد والهندسة، لكن التطورات اللاحقة للرياضيات شهدت نشوء فروع متعددة أهمها الجبر لحقها عملية تداخل الهندسة مع الجبر.[1]

 واما عن اقسامها فتنقسم الي الهندسة الاقليدسية وهي الهندسة التي تبحث في خواص لمكان ذي الأبعاد الثلاثة، والي الهندسة التي تتصور مكاناً هندسياً مختلفاً عن فضاء  إقليدس (كهندسة ريمان) وله عدد غير محدود من الأبعاد، فتسمى بـ الهندسة اللاقليدسية (Géométric non Euclidienne)، وهي أعم من الهندسة الإقليدسية، وأكثر منها تجريداً.

ﻵن لنستمع الي هيلبرت ومقدمة كتابه Foundations of Geometry حيث يقول :

التحقيق التالي هو محاولة جديدة لاختيار لهندسة مجموعة بسيطة وكاملة من المسلمات المستقلة تمكن من اسنتاج  النظريات ذات الطابع الهندسي الأكثر أهمية مع توخي أكبر قدر من الوضوح و ابراز  أهمية مجموعة  المسلمات و الاستنتاجات و التي يمكن الخروج من بها.

ثم يعقب قائلا في البداية دعونا نعتبر ثلاثة أنظمة مختلفة :

• الأشياء المكونة للنظام الأول، وسوف ندعوها نقاط ونرمز لها بالحروف A، B، C،. . . ،
•  وتلك  المكونة للنظام الثاني، وسوف ندعوها خطوط مستقيمة ونرمز لها بالحروف  .a  ،b ، c ،
• وتلك  المكونة للنظام الثالث، وسوف ندعوها المستويات ونرمز لها بالحروف اليونانية α، β، γ،. . . 

تشكل النقاط عناصر الهندسة الخطية، و تشكل النقاط والخطوط المستقيمة عناصرالهندسة المستوية، و تشكل النقاط والخطوط والمستويات، عناصر هندسة الفضاء أو العناصر المكونة للفضاء اﻷقليدي.

اجل بهذه البساطة ، ﻵن ربما نفكر ان هذه النثاط هذه الخطوط و هذه المستويات تربطها علاقات تحدد انظمتها و يمكن يوصفها بكلمات مثل التوازي ، التقاطع ، و اﻷنتماء ....

وهذا التفكير سليم تماما و يمكن القول ان مجموع تلك العلاقات تحكمها مجموعة من المسلمات سنتعرض لها بالتفصيل في تدينات لاحقة

اليوم سنقسم هذه المسلمات الي خمس مجموعات كل من هذه المجموعات تعبر، في حد ذاته، عن بعض الحقائق الأساسية ذات الصلة بحدسنا وبكيفية تطبيقنا لمنطق علي العالم الذي يحيط بنا.
 و هذه المجموعات هي  :

• مسلمات الترابط : هذه المجموعة تأسس لكيفية اتصال  المفاهيم المذكورة أعلاه، اي النقاط، الخطوط المستقيمة،و المستويات.
• مسلمات الترتيب : بديهيات لهذه المجموعة تحدد الفكرة التي تعبر عنها كلمة "بين"، وتجعل من الممكن، على أساس هذه الفكرة، وترتيب سلسلة من النقاط على خط مستقيم، في مستوي، وفي الفضاء.  وتحتم علي نقاط على خط مستقيم ان يكون لها علاقة معينة مع بعضها البعض.
• مسلمة التوازي او مسلمة اقليدس : إدخال هذه المسلمة يبسط إلى حد كبير المبادئ الأساسية للهندسة و هي التي تقول انه من نقطة معينة لا تنتمي لمستقيم معين لا يمكن رسم الا مستقيم واحد موزاي لذلك المستقيم.
• مسلمات التحاكي  : بديهيات لهذه المجموعة تعريف فكرة التحاكي أو الإزاحة.
• مسلمة ارخميدس او مسلمة اﻷتصال.

و سنواصل ان شاء الله في تدوينات لاحقة شرح هذه المسلمات و كيفية ترابطها مع بعضها ومع تعريفات المختلفة  لبناء الهندسة اﻷقليدية التي تحكم عالمنا.

  

تابع القراءة

0 [ فيديو] هل يمكن للنمل ان يعد ؟

النمل من عجائب خلق الله و امة من اﻷمم تتجلي فيها عظمة تصريف الخالق في ملكه و غرائب النمل لا تعد ولا تحصي و اعدادها لا يعلمها الا الله عز وجل
في هذا التدوينة سنكتشف احدي التجارب العلمية الجميلة لمعرفة ما اذا كان النمل يستطيغ ان يحسب ام لا.....

اما المناسبة فهو الفيديو الكارتوني الذي اعده Todd Rosenberg صاحب موقع OddTodd وعرض في وقت سابق في مؤتمرAPS March Meeting 2012 الذي يعتبر من اشهر مؤتمرات الفيزياء حول العالم....

وتناول فيه بطريقة شيقة كيف صمم العلماء تجربة لمعرفة هل النمل يعد ام لا ؟

في البداية لنستمع اولا للدكتور  أحمد مدحت إسلام‬  في كتابه   "لغة الكيمياء عند الكائنات الحية"[1] :
 ‫

 من المعروف ان من  أكثر أنظمة الاتصال الكيميائية تطورا‬ في الطبيعة، هي تلك الأنظمة التي تستخدمها بعض‬ ‫أفراد ملكة الحشرات الفائقة التنظيم مثل النحل‬ ‫أو النمل.‬....

ثم يعقب قائلا :

‫و لقد أثبتت الدراسات التي أجريت في هذا المجال أنه‬ عندما تعثر إحدى الشغالات على الغذاء أثناء تجوالها، فعـنـدمـا تـعـثـر‬ مثلا على حشرة ميتة أو أي شيء آخر يصلح غذاء لأبناء جنسهـا، تـتـنـاول‬ ‫منه قدرا كافيا ثم تبدأ في العودة إلى مكان تجمع النمل أو إلى االمستعمرة‬ كي تخطر بقية الأفراد بوجود وفـرة مـن الـغـذاء فـي هـذا ا لمـوقـع الجـديـد.‬ ‫وحتى لا تضل هذه الشغالة الطريق، تقوم أثناء عودتهـا بـوضـع مـادة تسمي ما د ة لأثـر‬ على سطح الأرض مبتدئة من موقع الغذاء حتى تصل إلى موقع المستعمرة‬ ‫وبذلك تكون قد رسمت لغيرها دون مجهود، الطريق الصحيح الذي يجـب‬ أن يسلكه كل من يريد الوصول إلى موقع الغذاء.‬

ولكن مواد اﻷثر يمكن استخدامها فقط في الغابة، وليس في بيئة صحراوية حيث تهب رياح عاتية ، تؤدي الي تشتيت مواد اﻷثر بسرعة و لذلك لابد ان للنمل من ان يتواصل بطريقة اخري و احدي الحلول الممكنة انها تعد خطاها حتي تصل الي الغذاء ثم تعدها مرة اخري بعد ان تعكس اﻷتجاه لكي تصل الي قريتها! و لكن كيف يمكن برهان ذلك العلماء صمموا تجربة لمعرفة هل النمل تعد ام لا وهذا فيديو يشرح ذلك لنتابع :

ﻷعداد هذه التجربة الجميلة قامت مجموعة من الباحثين بتدريب مجموعة من النمل على السير عبر الصحراء إلى بعض المواد الغذائية. و عندما بدأ النمل يأكل، يقسمها العلماء الي ثلاث مجموعات تركت المجموعة الأولى بدون تغير[2].

اما المجموعة الثانية، فقط وضعت ركائز متينة تحت على كل من سيقانها الست مما حعل سقانها اطول.

اما المجموعة الثالثة فقد تم قطع اجزاء من ارجلهم لجعل كل من السيقان أقصر من سيقان النمل العادي .

و بعد تناول وجبة ،أ فرج عن النمل ليعودو للقريتهم بينما راقب العلماء ليرو ما سيحدث....

رسم توضيحي ﻷرجل النمل الخاضعة لتجربة

مشى النمل العادي و لحق بالقرية.

مشى النمل ذو اﻷرجل الطويلة حتي تجاوز القرية وتوقف.

ومشي النمل ذو اﻷرجل القصيرة مسافة اقل من بعد القرية ، ثم توقفت عن البحث عن القرية.

اتضح أن كل النمل قد سار نفس العدد من الخطوات، و لكن لأنه تم تغيير اﻷرجل الخاصة بهم ( وبتالي تغير طول خطواتهم) ذهبوا بالضبط المسافات التي تم التكهن بها وفقا لنظرية ان أدمغتهم تحدد عدد الخطوات إلى الطعام ومن ثم عكس الاتجاه، وتحسب نفس العدد من الخطوات الى الوراء. وبعبارة أخرى، ان النمل تحسب نفس العدد من خطوات الى الوراء!





هل يعني ذلك النمل لديها شيء من قبيل عداد خطى لكي تقوم بالعد؟

يقول البروفيسور جيمس جولد من جامعة برينستون ، معلقا على هذه التجربة  : 

 انه من الواضح تماما ان النمل ليس لديهم خرائط في رؤوسهم، ولا تعرف علامات على طول الطريق. و هذه التجربة تشير بقوة إلى أن النمل لديهم عداد خطى داخلي الذي يسمح لهم بالعد و حتي الرجوع الي قريتهم بكل سهولة ....

فسبحان الذي خلق النمل و سبحان الذي علمها العد ...

_____________________________________________________________________
 [1] كتاب : لغة الكيمياء عند الكائنات الحية. لتحميله اضغط هنا 

[2] 2006, Matthias Wittlinger, et al. , "The Ant Odometer: Stepping on Stilts and Stumps ", Science 

تابع القراءة